Last Updated: May 2023 (Income Inequalities)
Income Inequalities
This article deals with ‘Income Inequalities.’ This is part of our series on ‘Economics’ which is an important pillar of the GS-2 syllabus. For more articles, you can click here.
Introduction
- Income inequality is the degree to which income or wealth holding is unevenly distributed throughout the population.
- It is measured statistically using Gini Coefficient.
- Apart from that, Oxfam also releases a report every year showing the income inequality in the world and India.
Gini Coefficient
- Gini Coefficient is a statistical measure to gauge income inequality or wealth divide.
- Its value varies between 0 to 1, 0 indicating perfect inequality and 1 indicating perfect equality.
- An increase in value of the Gini Coefficient means that inequality in an economy is increasing, and government policies are not inclusive and benefitting richer.
Calculation of Gini Coefficient
- Gini Coefficient = A / (A+B)
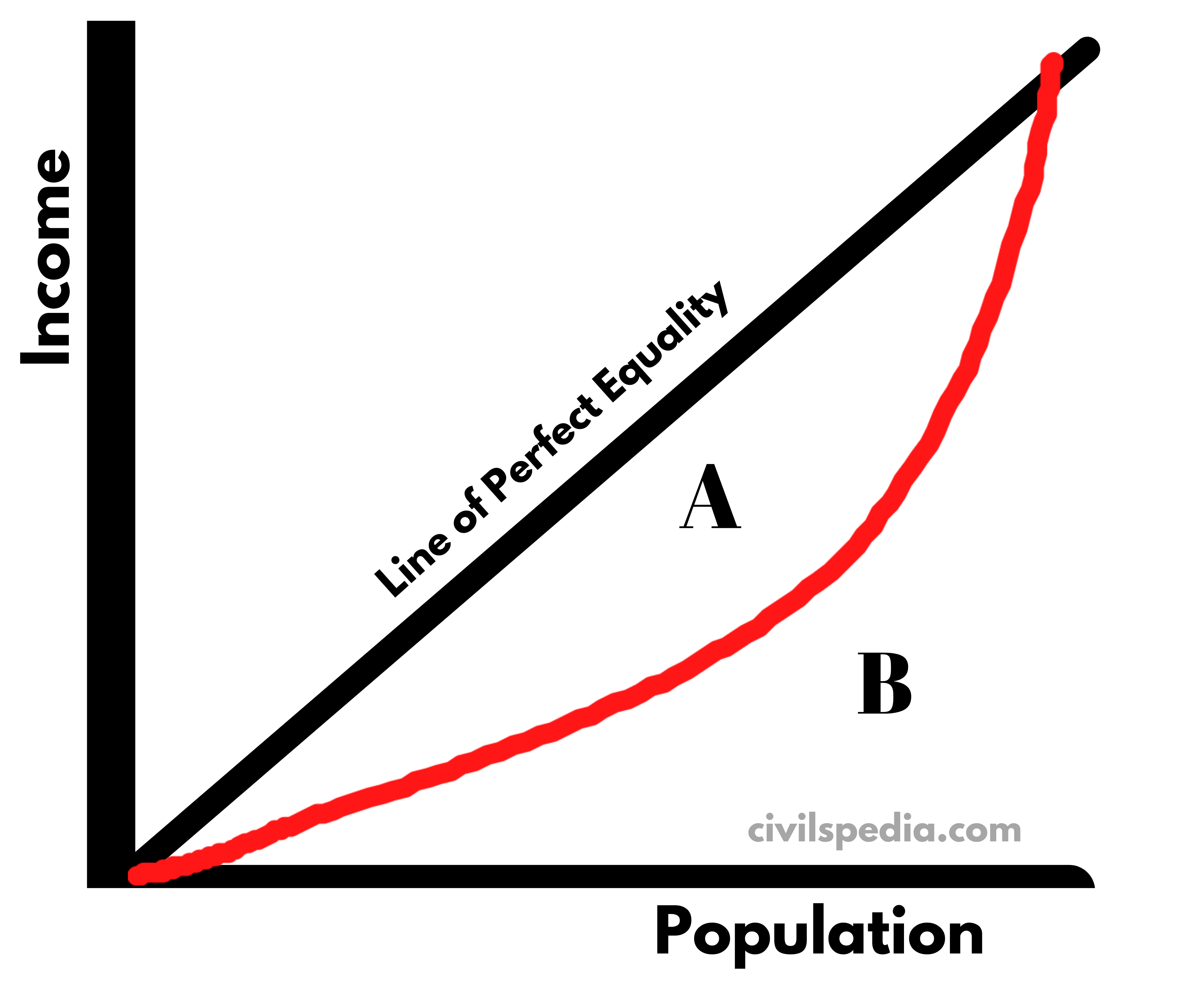
- In the graph shown above
- The horizontal axis on this chart represents cumulative shares of the population.
- The vertical axis is cumulative shares of income.
- A+ B is constant, and if
- A is higher; inequality is higher.
- A is smaller; inequality is lower.
- If A = 0, then no income inequality.
- Hence, Gini Coefficient is measured from 0 to 1, and the lower value means low inequality and higher means more inequality.
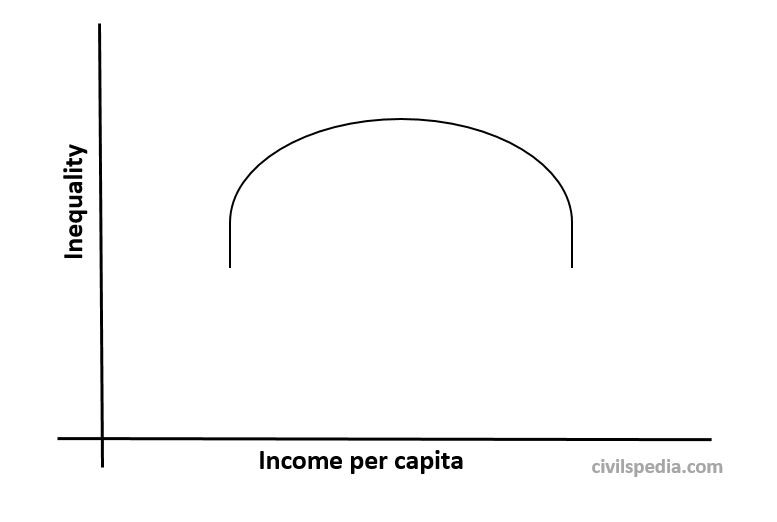
Kuznet Curve on Inequality
- Famous US Economist Simon Kuznet showed that market forces would first increase inequality and then decrease inequality among people as an economy develops.
- It happens because the initial phase of economic growth boosts the income of workers and investors who participate in the first wave of innovation. But this inequality is temporary as other workers and investors soon catch up, resulting in improvement of their incomes as well.
Palma Ratio
- It is the ratio of the percentage of income earned by the richest 10% with the percentage of income earned by the poorest 40%.
- For India, this ratio is approximately 1.5.
Quintile Ratio
- It is the ratio of income of the richest 10% and poorest 10% in an economy.
- In the case of India, the income of the richest 20% is 45% of total income, and the poorest 20% is 8% of total income. Hence, the Quintile Ratio of India is 5.6.
India and Income Inequality
- Piketty, the world-famous economist, has cautioned India for rising levels of Income inequalities and their consequences. In countries like India, where other forms of inequalities are present, like the caste system, income inequalities exacerbate the situation.
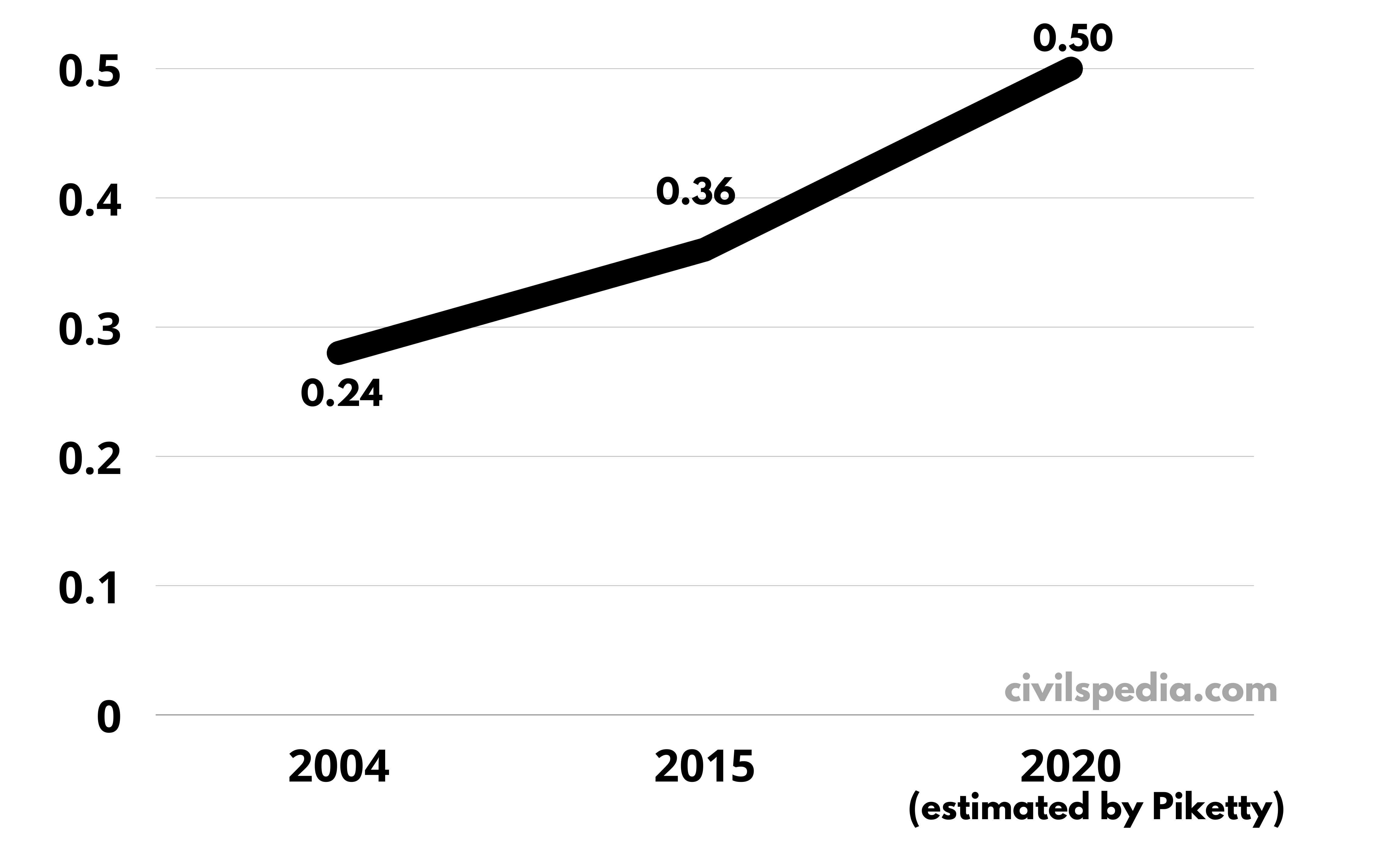
- India grew at an average rate of 7.5% since 2011, but growth is not equally distributed (the rich are growing more). Gini Coefficient shows that income inequality is continuously increasing in India. The following data about India’s Gini Coefficient corroborates this.
- According to Oxfam Report (2020), India’s top 1% wealthy people hold 42% of the National Wealth while the bottom 60% own less than 5%.
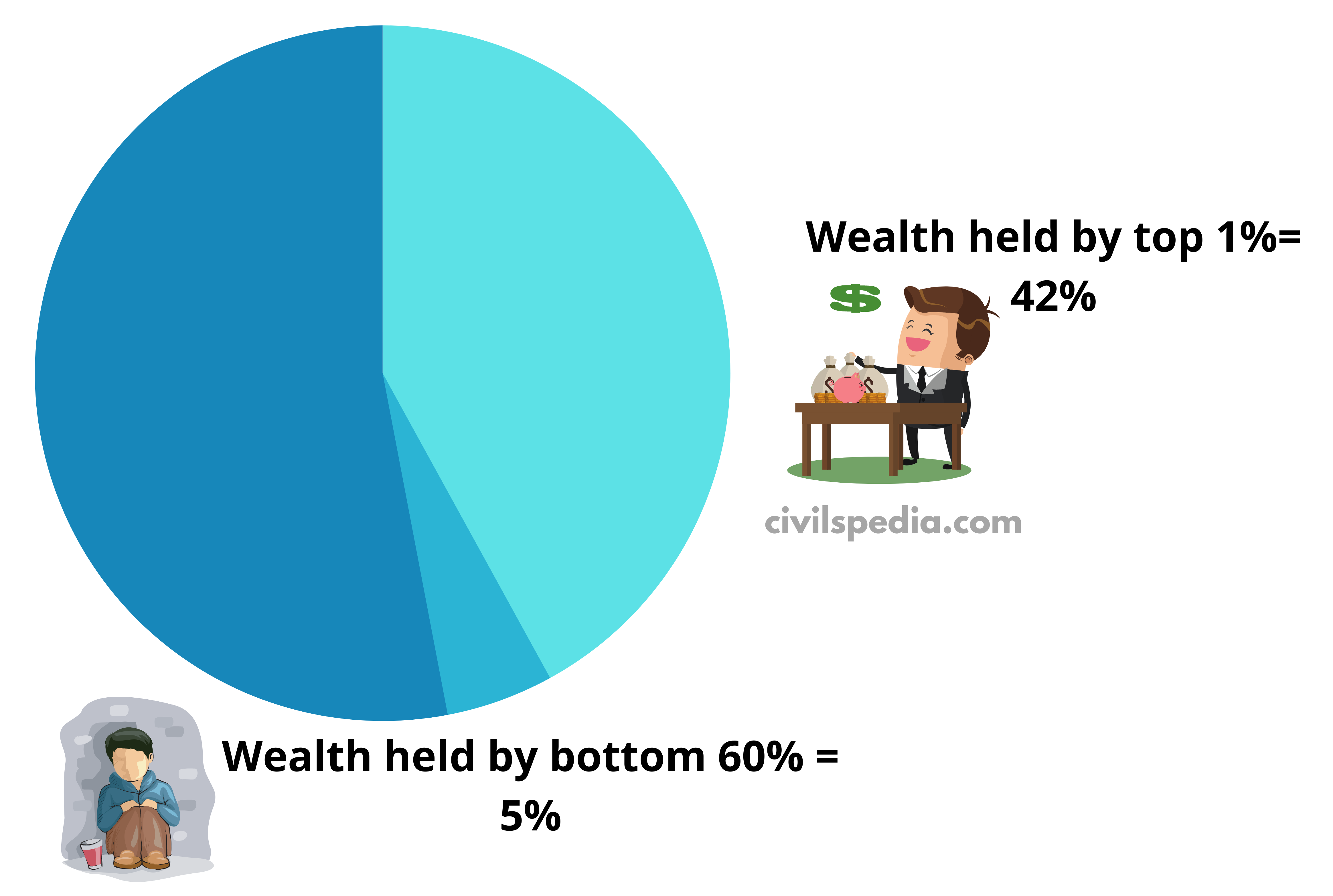
- According to Oxfam head, it is morally outrageous that a few wealthy individuals are collecting a growing share of India’s wealth while the poor struggle to find their next meal. If this obscene inequality continues, it will lead to a complete collapse of the country’s social and democratic structure.
- According to the World Inequality Report (2022) released by the World Inequality Lab of the Paris School of Economics
- It termed India as a ‘poor and very unequal country, with an affluent elite’.
- The top 10% of the Indian population holds 57% of national income, including 22% held by the top 1%
- The bottom 50% of the Indian population holds just 13% of national income.
- The report has suggested levying a modest progressive wealth tax on multimillionaires.
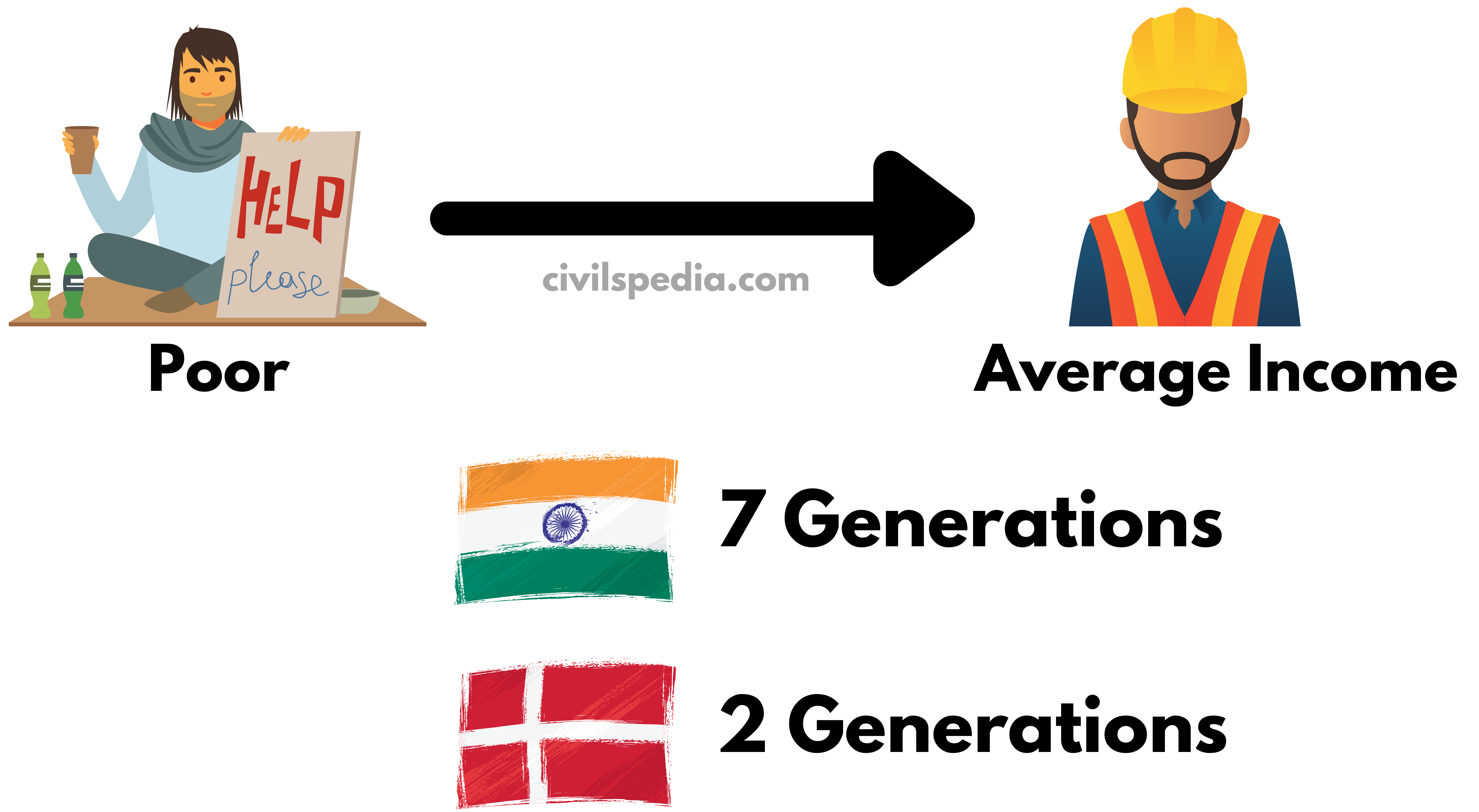
- According to the Global Social Mobility report released by the World Economic Forum, the poor in India are more likely to remain poor. It would take 7 generations in India while 2 generations in Denmark for the poor to reach average income.
- Further, the Covid pandemic has deepened inequalities of wealth, education, and gender as shown by Oxfam’s report.
Causes of Income Inequality
1. Historical Causes
- Caste System: Due to the exclusion of lower caste from ownership of land and education, people belonging to lower caste are poor.
2. Social Causes
Due to the patriarchal and patrilineal nature of Indian society, women don’t own factors of production in India.
3. Frequent Global Economic Crisis
- Economic crises like that of 2008 accentuate income inequality by making richer rich and poorer poor. (How= Central Bank cant allow big houses to fall. Due to this, business houses get significant cuts. Currency devaluates, and the loans that companies have to pay decrease in reality. On the other hand, households who deposit their money lose the value of their money).
4. Faulty Taxation System
- In India, there is more reliance on Indirect Tax, which is regressive in nature.
- Inheritance tax, which is levied when wealth is inherited from one generation to another, is almost negligible in India.
5. Cantillon Effect
The Cantillon Effect is a concept that describes ways in which changes in the money supply can affect different groups of people and economic sectors unequally.
Imagine a situation where the government decides to print additional money and put it into circulation.
- The first people or institutions to receive this new money, such as banks or wealthy individuals, have an advantage because they can spend it before prices rise.
- Later, when the money flow increases in the whole economy, it leads to inflation. People who receive the new money later, such as workers or those on fixed incomes, may find that their purchasing power has decreased.
So, the Cantillon Effect suggests that those who are closer to the source of new money creation benefit the most, while those further away experience the negative consequences of inflation. This can result in wealth redistribution and income inequality.
6. India relied on Trickle-Down Approach
- India relied on the ‘Trickle Down Approach’, which benefitted the industrial houses and rich businessmen. Instead, in order to reduce inequality, India should have followed the redistributive justice principles of John Rawls, Gandhian trusteeship principles or Amartya Sen’s capability approach.
7. Technological Change
- Rapid technological changes are leading to the automation of industries. As a result, few people with high skills are getting high packages while many workers are losing their jobs.
8. Capture of power by elites
- Due to Crony Capitalism, political leaders and government work as agents of elites. Policies of government are made to benefit elite sections of society.
Consequences of Inequalities
1. Conflicts and Insurgency
- Arab Spring of 2011 in the Middle East was the result of high inequalities in that region.
- Earlier in India, Naxalbari Movement was the result of inequality (in landholding).
2. Divides Society
- It divides society between haves and have-nots. For India, with an already fractured society over religion, region, gender, or caste, inequality adds another fracture point.
- The work of Piketty reveals that when inequalities increase intolerably, governments divide to rule, and persecution of minorities increases with the politics of national identities.
3. Increase in Crimes
- It has been observed that unequal societies have higher crime rates. Poverty force people to earn via illegal means.
4. Political Impacts
- In case of higher inequalities, political democracy and government lose their legitimacy.
5. Effects on Growth
- Income distribution matters for growth. If income is more equally distributed, more potential buyers of goods create bigger markets.
Steps Taken by India
1. Land Reforms
- The government introduced the land reforms and abolished the Zamindari System for equitable distribution of the land in the country.
2. Tax Reforms
- Piketty has suggested India should improve its Tax: GDP, which is abysmally low. The Indian government is taking steps to bring more people into the tax net.
- Apart from that, India has a progressive system of taxation. Progressive Taxation system helps in ‘redistribution of money’ from richer to less well off.
3. Skill Development
- Improving education quality, eliminating financial barriers to higher education, and supporting apprenticeship programmes.
4. Social Security
The high cost of healthcare and medicines drives a hundred million people into poverty every year. There must be a universal and permanent safety net for the poorest and most vulnerable. The government has taken various measures like starting the Ayushman Bharat Scheme.
5. Various steps against Black money
The government has taken steps like demonetisation to control black money.
Way Ahead
- Universal Basic Income: Introduce universal basic income (as recommended by Economic Survey 2016-17) and raise the minimum income of the common public. These measures can reduce the income gap and result in equal distribution of earnings in the labour market.
- Urban Employment Guarantee Schemes: Urban counterpart of MGNREGS, which is demand-based and offers guaranteed employment, should be introduced to rehabilitate surplus labour.
- Equitable access to education: Enhance the budgetary allocation for education to 6% of GDP, as committed in the National Education Policy, and the creation of more jobs with long-term growth are vital for triggering upward mobility among people experiencing poverty.
- Rationalization of Subsidies: Better targeting of beneficiaries through alternatives like direct benefit transfers over existing inefficient mechanisms
Case Study: Wealth Redistribution Council
- In 2021, Japanese PM Kishinev announced the creation of the ‘Wealth Redistribution Council‘ to tackle rising wealth inequalities and redistribute the wealth among households.
- Japan aims to pass on wealth from corporations to the households to double the household incomes and rebuild a broader middle class. It will also help in recovering the Japanese economy post-Covid pandemic.
